Definimos escala de um desenho como sendo a razão entre o comprimento do projeto e o comprimento real correspondente,
sempre medidos na mesma unidade:
Usamos escala quando queremos representar um esboço gráfico de objetos, da planta de uma casa ou de uma cidade, mapas,
maquetes, etc.
Se num mapa a escala indicada é de 1 : 1000, isso quer dizer que cada medida no desenho do mapa é 1000 vezes menor que a
realidade, sendo assim : Cada 1 cm medido no mapa representará no real ->1000 cm = 10 m
Se num projeto arquitetônico cada cm desenhado equivale a 120 cm ( 1,2 m ) de dimensão real, afirmamos que esse modelo está
na escala de 1 : 120, ou seja, tudo na realidade é 120 vezes maior que no projeto arquitetônico.
Se num aeromodelo cada cm do protótipo equivale a 32 cm no real, afirmamos que esse modelo está na escala de 1 : 32, ou seja,
tudo no avião é 32 vezes maior que no modelo.
domingo, 29 de agosto de 2010
Número Racionais
Números Racionais
Interseção dos conjuntos: Naturais, Inteiros e Racionais.
Os números decimais são aqueles números que podem ser escritos na forma de fração.
Podemos escrevê-los de algumas formas diferentes:
Por exemplo:
♦ Em forma de fração ordinária: ; ; e todos os seus opostos.
Esses números tem a forma com a , b Z e b ≠ 0.
♦ Números decimais com finitas ordens decimais ou extensão finita:
Esses números têm a forma com a , b Z e b ≠ 0.
♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:
As dízimas periódicas de expansão infinita, que podem ser escritas na forma : com a, b Z e b ≠ 0.
► O conjunto dos números racionais é representado pela letra Q maiúscula.
Q = {x = , com a Z e b Z*}
►Outros subconjuntos de Q:
Além de N e Z, existem outros subconjuntos de Q.
Q* ---------- É o conjunto dos números racionais diferentes de zero.
Q+ ---------- É o conjunto dos números racionais positivos e o zero.
Q- ----------- É o conjunto dos números racionais negativos e o zero.
Q*+ ---------- É o conjunto dos números racionais positivos.
Q*- ----------- É o conjunto dos números racionais negativos.
► Representação Geométrica
Entre dois números racionais existem infinitos outros números racionais.
Interseção dos conjuntos: Naturais, Inteiros e Racionais.
Os números decimais são aqueles números que podem ser escritos na forma de fração.
Podemos escrevê-los de algumas formas diferentes:
Por exemplo:
♦ Em forma de fração ordinária: ; ; e todos os seus opostos.
Esses números tem a forma com a , b Z e b ≠ 0.
♦ Números decimais com finitas ordens decimais ou extensão finita:
Esses números têm a forma com a , b Z e b ≠ 0.
♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:
As dízimas periódicas de expansão infinita, que podem ser escritas na forma : com a, b Z e b ≠ 0.
► O conjunto dos números racionais é representado pela letra Q maiúscula.
Q = {x = , com a Z e b Z*}
►Outros subconjuntos de Q:
Além de N e Z, existem outros subconjuntos de Q.
Q* ---------- É o conjunto dos números racionais diferentes de zero.
Q+ ---------- É o conjunto dos números racionais positivos e o zero.
Q- ----------- É o conjunto dos números racionais negativos e o zero.
Q*+ ---------- É o conjunto dos números racionais positivos.
Q*- ----------- É o conjunto dos números racionais negativos.
► Representação Geométrica
Entre dois números racionais existem infinitos outros números racionais.
sexta-feira, 27 de agosto de 2010
Razão
Chama-se de razão entre dois números racionais a e b, com b ¹ 0, ao quociente entre eles. Indica-se a razão de a para b por a/b ou a : b.
Exemplo:
Na sala da 6ª B de um colégio há 20 rapazes e 25 moças. Encontre a razão entre o número de rapazes e o número de moças. (lembrando que razão é divisão)
Voltando ao exercício anterior, vamos encontrar a razão entre o número de moças e rapazes.
Termos de uma Razão

Proporção
A igualdade entre duas razões forma uma proporção, vale lembrar que razão é a divisão entre dois números a e b, tal que b ≠ 0 e pode ser escrito na forma de a/b. Observe os exemplos de proporções a seguir:
.jpg) é uma proporção, pois 10:20 = 3:6
é uma proporção, pois 10:20 = 3:6
.jpg) é uma proporção, pois 9:12 = 3:4
é uma proporção, pois 9:12 = 3:4
As proporções possuem uma propriedade que diz o seguinte: “em uma proporção, o produto dos extremos é igual ao produto dos meios.” Essa propriedade pode ser colocada em prática na verificação da proporcionalidade, realizando uma operação denominada multiplicação cruzada.
.jpg)
9 x 4 = 12 x 3
36 = 36
Multiplicação cruzada
.jpg)
4 x 15 = 6 x 10
60 = 60
As proporções possuem uma enorme aplicabilidade em situações problemas envolvendo informações comparativas, na regra três a proporcionalidade é usada no intuito de calcular o quarto valor com base nos três valores estabelecidos pelo problema. Acompanhe os exemplos a seguir no intuito de demonstrar a importância do estudo das proporções.
Exemplo 1
Para fazer 600 pães, são gastos, em uma padaria, 100 Kg de farinha. Quantos pães podem ser feitos com 25kg de farinha?
Estabelecemos a seguinte relação:
600 -------------- 100
x -------------- 25
60 = 60
Exemplo 1
Para fazer 600 pães, são gastos, em uma padaria, 100 Kg de farinha. Quantos pães podem ser feitos com 25kg de farinha?
Estabelecemos a seguinte relação:
600 -------------- 100
x -------------- 25
.jpg)
Podem ser feitos 150 pães.
Exemplo 2
Se com 40 laranjas é possível fazer 26 litros de suco, quantos litros de suco serão obtidos com 25 laranjas?
40 -------- 26
25 -------- x
.jpg)
Com 25 laranjas podemos fazer 16,25 litros de suco.
Inequação do 1 grau
INEQUAÇÕES DO 1º GRAU
* Definição
Em sua definição mais simples e compreensível, pode ser definida como toda e qualquer sentença da matemática que é aberta por um sinal de desigualdade.

Sendo que: a e b, são números reais e diferentes de zero (a e b ≠ 0), respectivamente.
Exemplos:
2x – 8 > 0 4x + 9 ≥ 0
3x – 9 < 0 5x + 1 ≤ 0
3
3
* O que representa os sinais das inequações

* Observações gerais sobre Inequações
Observando as condições de vida da população do Brasil, obviamente encontraremos um grande mar de desequilíbrio. Estas desigualdades podem ser encontradas em diversas áreas, mais a que mais de destacam são social e econômica.
* Solução de inequações do 1º grau
Nas equações do primeiro grau que estejam na forma ax + b > 0, tem-se o objetivo de se apurar um conjunto de todas e quaisquer possíveis valores que possam assumir uma ou mais variável que estejam envolvidas nas equações proposta no problema.
Acompanhe:
Determine todos os possíveis números inteiros positivos para os quais satisfaça a inequação:
3x + 5 < 17
Veja os seguintes passos para solução:

Após fazer os devidos cálculos da inequação acima, pode-se concluir que a solução apresentada é formada por todos os números inteiros positivos menores que o número 4.
S = {1, 2, 3,}
* Exemplos de fixação de conteúdo
a) 2 -4x ≥ x + 17
Solução:

b) 3(x + 4) < 4(2 –x)
Solução:

c) Quais os valores de X que tornam a inequação -2x +4 > 0 verdadeira?
Solução:

O número 2 não é a solução da inequação dada, mais sim qualquer valor menor que 2.
Verifique a solução:
Para x = 1
-2x +4 > 0
-2.(1) +4 > 0
-2 + 4 > 0
2 > 0 ( verdadeiro )
Observe, então, que o valor de X menor que 2 é a solução para inequação.
* Propriedades da inequação do 1º grau
Quando uma equação do 1º grau é resolvida, são usados os recursos matemáticos tais como: somar ou diminuir um valor igual aos dos componentes da equação ou multiplicar e dividir os membros componentes da equação por um mesmo valor.
Será que é possível usar estes mesmo recursos de soluções das equações para resolver as inequações do primeiro grau ?
Analise os exemplos:
Inequação
5 > 3
Recurso:
5 > 3 ( somar o valor 2 )
5 + 2 > 3 + 2
7 > 5 (continua sendo uma inequação verdadeira)
Inequação
5 > 3
Recurso:
5 > 3 (subtrair 1)
5-1 > 3 -1
4 > 2 (continua sendo uma inequação verdadeira)
Desta forma, é possível concluir que de acordo com as propriedades das equações de primeiro grau, podemos usar os mesmos recursos matemáticos de somar ou subtrair um mesmo valor aos membros da inequação do primeiro grau.
Analise os exemplos:
Inequação
5 > 3
Recurso:
5 > 3 (multiplicar pelo valor positivo 2)
5 x (+2) > 3 x (+2)
10 > 6 (continua sendo uma inequação verdadeira)
Inequação
5 > 2
Recurso:
5 > 2 (multiplicar pelo valor negativo -2)
(-2).5 > 2.(-2)
-10 > -4 (a inequação não é verdadeira)
Para que a inequação acima se torne verdadeira é preciso inverter o sinal.
-10 < -4 (agora a inequação é verdadeira)
Portanto, é preciso ter o máximo de cuidado ao utilizar o recurso matemático de (multiplicar ou dividir por um mesmo valor os componentes da inequação) para resolver uma inequação do primeiro grau. Caso este valor seja um número negativo, o sinal da desigualdade (inequação) deve ser invertido.
quinta-feira, 26 de agosto de 2010
Expressões Numéricas
Expressões numéricas
Uma expressão numérica é uma seqüência de números associados por operações. Essas operações devem ser efetuadas respeitando-se a seguinte ordem:
1) Potenciações e radiciações, se houver.
2) Multiplicações e divisões, se houver.
3) Adições e subtrações
Exemplo:
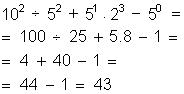
Em expressões numéricas com sinais de associação ( parênteses, colchetes e chaves) efetuam-se, primeiro as operações dentro dos parênteses, depois as que estão dentro dos colchetes e, por último, as interiores as chaves, respeitando-se ainda, a prioridade das operações.
Exemplo:
36 + 2.{25 + [ 18 – (5 – 2).3]} =
= 36 + 2.{ 25 + [18 – 3.3]} =
= 36 + 2.{25 + [18 – 9]} =
= 36 + 2.{25 + 9} =
= 36 +2.34 =
= 36 + 68 = 104
Outro exemplo:
[(5² - 6.2²).3 + (13 – 7)² : 3] : 5 =
= [(25 – 6.4).3 + 6² : 3] : 5 =
=[(25 – 24).3 + 36 : 3 ] : 5 =
= [1.3 + 12] : 5 =
= [3 + 12 ] : 5 =
= 15 : 5 = 3
Efetue:
11 + 32 + 4.9 – 15 : 3 =
11 + 32 + 36 – 5 = 74
109 – 15.4 + 26 : 13 =
109 – 60 + 2 = 51
10 + 3502 : 17 – 100 : 25 =
10 + 206 – 4 = 212
25 + 25 : 25 – 25.1 =
25 + 1 – 25 = 1

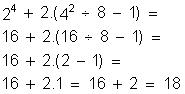

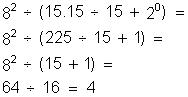

(7.6 – 32 : 2) : 13 =
(42 – 16 ) :13 =
26 : 13 = 2

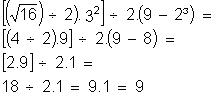

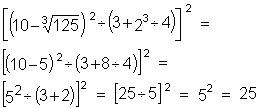
Calcule o valor numérico das expressões:
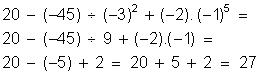

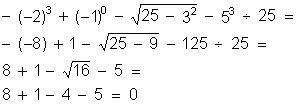

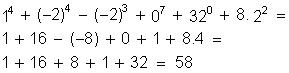

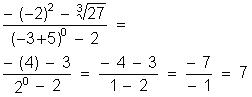

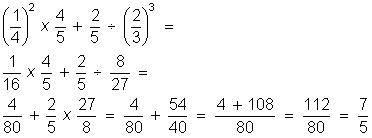

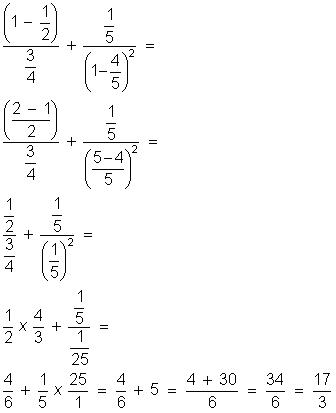

(0,5)² : 5 – 2.(0,3.1,2 - 0,72 : 2,4) =
0,25 : 5 – 2. (0,36 – 0,3) =
0,05 – 2.(0,06) =
0,05 – 0,12 = - 0,07

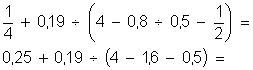




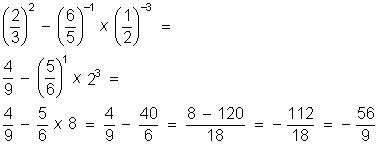

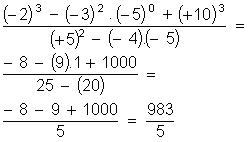

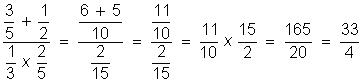

(- 3,5 + 2.1,45) – ( -1,2 : 5 – 3,5) =
(-3,5 + 2,9 ) – (-0,24 – 3,5) =
-0,6 – (-3,74) =
-0,6 + 3,74 = 3,14

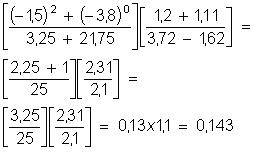

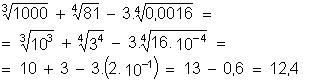

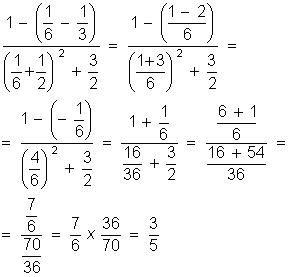

Considere a expressão
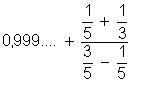
Efetuando as operações indicadas e simplificando, temos:
a) 9/10 d) 15/9
b) 7/3 e) 1
c) 19/10
Solução:
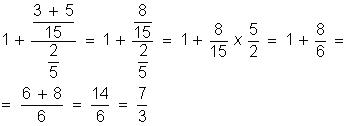
Alternativa correta: (b)
Simplifique:
Assinar:
Postagens (Atom)